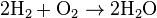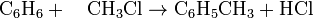(
- N2 + 3H2 → 2NH3
Reaction stoichiometry describes the quantitative relationships among substances as they participate in chemical reactions. In the example above, reaction stoichiometry describes the 1:3:2 ratio of molecules of nitrogen, hydrogen, and ammonia.
Composition stoichiometry describes the quantitative (mass) relationships among elements in compounds. For example, composition stoichiometry describes the nitrogen to hydrogen (mass) relationship in the compound ammonia: i.e., one mole of nitrogren and three moles of hydrogen are in every mole of ammonia.
A stoichiometric amount or stoichiometric ratio of a reagent is the amount or ratio where, assuming that the reaction proceeds to completion:
- all reagent is consumed,
- there is no shortfall of reagent, and
- no residues remain.
While almost all reactions have integer-ratio stoichiometry in amount of matter units (moles, number of particles), some nonstoichiometric compounds are known that cannot be represented by a ratio of well-defined natural numbers. These materials therefore violate the law of definite proportions that forms the basis of stoichiometry along with the law of multiple proportions.
Gas stoichiometry deals with reactions involving gases, where the gases are at a known temperature, pressure, and volume, and can be assumed to be ideal gases. For gases, the volume ratio is ideally the same by the ideal gas law, but the mass ratio of a single reaction has to be calculated from the molecular masses of the reactants and products. In practice, due to the existence of isotopes, molar masses are used instead when calculating the mass ratio.
Contents[hide] |
[edit] Etymology
"Stoichiometry" is derived from the Greek words στοιχεῖον (stoicheion, meaning element]) and μέτρον (metron, meaning measure.) In patristic Greek, the word Stoichiometria was used by Nicephorus to refer to the number of line counts of the canonical New Testament and some of the Apocrypha.[edit] Definition
Stoichiometry rests upon the very basic laws which help to understand it better i.e law of conservation of mass, the law of definite proportions (i.e., the law of constant composition) and the law of multiple proportions. In general, chemical reactions combine in definite ratios of chemicals. Since chemical reactions can neither create nor destroy matter, nor transmute one element into another, the amount of each element must be the same throughout the overall reaction. For example, the amount of element X on the reactant side must equal the amount of element X on the product side.Stoichiometry is often used to balance chemical equations (reaction stoichiometry). For example, the two diatomic gases, hydrogen and oxygen, can combine to form a liquid, water, in an exothermic reaction, as described by the following equation:
The term stoichiometry is also often used for the molar proportions of elements in stoichiometric compounds (composition stoichiometry). For example, the stoichiometry of hydrogen and oxygen in H2O is 2:1. In stoichiometric compounds, the molar proportions are whole numbers.
Stoichiometry is not only used to balance chemical equations but also used in conversions, i.e., converting from grams to moles, or from grams to millilitres. For example, to find the number of moles in 2.00 g of NaCl, one would do the following:
[edit] Different stoichiometries in competing reactions
Often, more than one reaction is possible given the same starting materials. The reactions may differ in their stoichiometry. For example, the methylation of benzene (C6H6), through a Friedel-Crafts reaction using AlCl3 as catalyst, may produce singly methylated (C6H5CH3), doubly methylated (C6H4(CH3)2), or still more highly methylated products, as shown in the following example,
products, as shown in the following example,[edit] Stoichiometric coefficient
In layman's terms, the stoichiometric coefficient (or stoichiometric number in the IUPAC nomenclature[1]) of any given component is the number of molecules which participate in the reaction as written.For example, in the reaction CH4 + 2 O2 → CO2 + 2 H2O, the stoichiometric coefficient of CH4 would be 1 and the stoichiometric coefficient of O2 would be 2.
In more technically-precise terms, the stoichiometric coefficient in a chemical reaction system of the i–th component is defined as
The extent of reaction ξ can be regarded as a real (or hypothetical) product, one molecule of which is produced each time the reaction event occurs. It is the extensive quantity describing the progress of a chemical reaction equal to the number of chemical transformations, as indicated by the reaction equation on a molecular scale, divided by the Avogadro constant (it is essentially the amount of chemical transformations). The change in the extent of reaction is given by dξ = dnB/nB, where nB is the stoichiometric number of any reaction entity B (reactant or product) an dnB is the corresponding amount.[2]The stoichiometric coefficient νi represents the degree to which a chemical species participates in a reaction. The convention is to assign negative coefficients to reactants (which are consumed) and positive ones to products. However, any reaction may be viewed as "going" in the reverse direction, and all the coefficients then change sign (as does the free energy). Whether a reaction actually will go in the arbitrarily-selected forward direction or not depends on the amounts of the substances present at any given time, which determines the kinetics and thermodynamics, i.e., whether equilibrium lies to the right or the left.
If one contemplates actual reaction mechanisms, stoichiometric coefficients will always be integers, since elementary reactions always involve whole molecules. If one uses a composite representation of an "overall" reaction, some may be rational fractions. There are often chemical species present that do not participate in a reaction; their stoichiometric coefficients are therefore zero. Any chemical species that is regenerated, such as a catalyst, also has a stoichiometric coefficient of zero.
The simplest possible case is an isomerism
There are usually multiple reactions proceeding simultaneously in any natural reaction system, including those in biology. Since any chemical component can participate in several reactions simultaneously, the stoichiometric coefficient of the i–th component in the k–th reaction is defined as
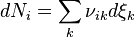 .
.
With complex reaction systems, it is often useful to consider both the representation of a reaction system in terms of the amounts of the chemicals present { Ni } (state variables), and the representation in terms of the actual compositional degrees of freedom, as expressed by the extents of reaction { ξk }. The transformation from a vector expressing the extents to a vector expressing the amounts uses a rectangular matrix whose elements are the stoichiometric coefficients [ νi k ].
The maximum and minimum for any ξk occur whenever the first of the reactants is depleted for the forward reaction; or the first of the "products" is depleted if the reaction as viewed as being pushed in the reverse direction. This is a purely kinematic restriction on the reaction simplex, a hyperplane in composition space, or N‑space, whose dimensionality equals the number of linearly-independent chemical reactions. This is necessarily less than the number of chemical components, since each reaction manifests a relation between at least two chemicals. The accessible region of the hyperplane depends on the amounts of each chemical species actually present, a contingent fact. Different such amounts can even generate different hyperplanes, all of which share the same algebraic stoichiometry.
In accord with the principles of chemical kinetics and thermodynamic equilibrium, every chemical reaction is reversible, at least to some degree, so that each equilibrium point must be an interior point of the simplex. As a consequence, extrema for the ξ's will not occur unless an experimental system is prepared with zero initial amounts of some products.
The number of physically-independent reactions can be even greater than the number of chemical components, and depends on the various reaction mechanisms. For example, there may be two (or more) reaction paths for the isomerism above. The reaction may occur by itself, but faster and with different intermediates, in the presence of a catalyst.
The (dimensionless) "units" may be taken to be molecules or moles. Moles are most commonly used, but it is more suggestive to picture incremental chemical reactions in terms of molecules. The N's and ξ's are reduced to molar units by dividing by Avogadro's number. While dimensional mass units may be used, the comments about integers are then no longer applicable.
[edit] Stoichiometry matrix
In complex reactions, stoichiometries are often represented in a more compact form called the stoichiometry matrix. The stoichiometry matrix is denoted by the symbol, .
.If a reaction network has n reactions and m participating molecular species then the stoichiometry matrix will have corresponding m rows and n columns.
For example, consider the system of reactions shown below:
- S1 → S2
- 5S3 + S2 → 4S3 + 2S2
- S3 → S4
- S4 → S5.
Often the stoichiometry matrix is combined with the rate vector, v to form a compact equation describing the rates of change of the molecular species:
[edit] Gas stoichiometry
Gas stoichiometry is the quantitative relationship (ratio) between reactants and products in a chemical reaction with reactions that produce gases. Gas stoichiometry applies when the gases produced are assumed to be ideal, and the temperature, pressure, and volume of the gases are all known. The ideal gas law is used for these calculations. Often, but not always, the standard temperature and pressure (STP) are taken as 0°C and 1 bar and used as the conditions for gas stoichiometric calculations.Gas stoichiometry calculations solve for the unknown volume or mass of a gaseous product or reactant. For example, if we wanted to calculate the volume of gaseous NO2 produced from the combustion of 100 g of NH3, by the reaction:
- 4NH3 (g) + 7O2 (g) → 4NO2 (g) + 6H2O (l)
-
PV = nRT V 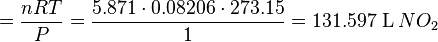
 and
and 
| where: | |
| P | = absolute gas pressure |
|---|---|
| V | = gas volume |
| n | = number of moles |
| R | = universal ideal gas law constant |
| T | = absolute gas temperature |
| ρ | = gas density at T and P |
| m | = mass of gas |
| M | = molar mass of gas |
[edit] Stoichiometric air-fuel ratios of common fuels
| Fuel | By mass [3] | By volume [4] | Percent fuel by mass |
|---|---|---|---|
| Gasoline | 14.6 : 1 | — | 6.8% |
| Natural gas | 14.5 : 1 | 9.7 : 1 | 5.8% |
| Propane (LP) | 15.67 : 1 | 23.9 : 1 | 6.45% |
| Ethanol | 9 : 1 | — | 11.1% |
| Methanol | 6.47 : 1 | — | 15.6% |
| Hydrogen | 34.3 : 1 | 2.39 : 1 | 2.9% |
| Diesel | 14.5 : 1 | 0.094 : 1 | 6.8% |
question :
1. Why do we care about Stoichiometry ?
2. How stoichiometric reaction between mercapto silica hybrids with hydrogen peroxide?